Diffraction is the slight bending of light as it passes around the edge of an object. The amount of bending depends on the relative size of the wavelength of light to the size of the opening. If the opening is much larger than the light's wavelength, the bending will be almost unnoticeable.

When light passes through a single slit of width \(a\) which is of the order of wavelength of light, then single slit diffraction is observed on a screen that is at distance \(D \gg a\).

The diffraction pattern is produced due to the interference of waves.

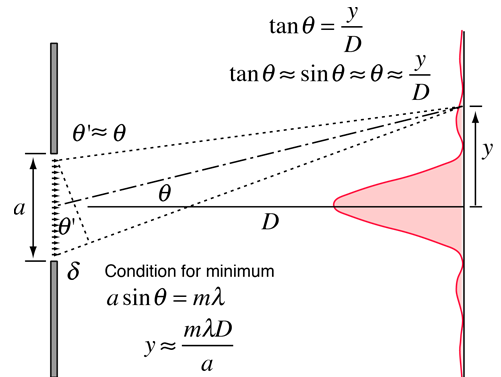
From the figure, \(\tan \theta = \frac{y}{D}\). Assuming \(\theta\) to be very small we get \(\theta \approx \tan \theta = \sin \theta\)
So we have, $$\theta = \frac{y}{D}$$

For a constructive interference pattern,

$$a \sin \theta = m \lambda $$ So $$a \frac{y}{D} = m \lambda$$ i.e. $$\lambda = \frac{ay}{mD}$$ where:
\(\lambda\) is wavelength of light
\(y\) is fringe width of first order maxima
\(D\) is distance between slit and screen
\(m\) is order of maxima