Three physical quantity need to be measured with reference to the white light.
|
S.No |
Physical quantity |
Independent/dependent |
Measured with |
Measuring instrument’s |
||
|
Minimum (m) |
Maximum (m) |
Least count
|
||||
|
1 |
\(\theta\) |
Dependent |
Circular scale with Vernier calipers |
\(0.5^{\circ}\) |
\(360^{\circ}\) |
\(30^{''}\) |
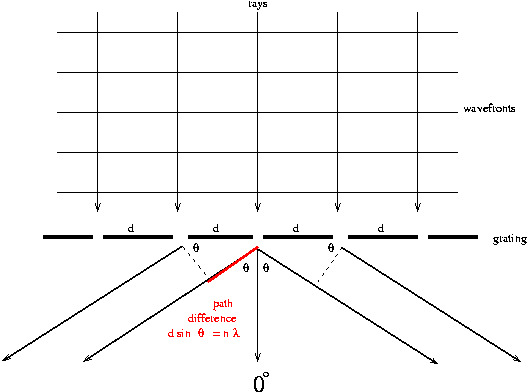
- Adjust the slit width to get the sufficient intensity through slit.
- Align the collimator, grating, telescope in such a way that we can see different wavelengths (colors) through the telescope lens.
- Record \(\theta_{w}\) of white light for right side, then record \(\theta_{1}\) (right side of white light) for different colors.
- Repeat the above step for the left side of white light and take it as \(\theta_{2}\) (left side of white light), including \(\theta_{w}\) for left.
- Subtract the \(\theta_{1}\) angles from \(\theta_{w}\) of corresponding side and take it as \(\theta_{1}^{'}\), repeat the same thing for \(\theta_{2}\) angles and take it as \(\theta_{2}^{'}\) .
- Take the average of the \(\theta_{1}^{'}\) and \(\theta_{2}^{'}\). Denote this as \(\theta\) and then substitute in \(\sin\theta\)
TABLES FOR RECORDING THE DATA
-
S.No.
Color
\(\theta_{1}\)
\(\theta_{2}\)
\(\theta_{1}^{'}\)
\(\theta_{2}^{'}\)
\(\theta = \frac{\theta_{1}^{'}+\theta_{2}^{'}}{2}\)
\( \sin \theta \)
\( \lambda = \frac{a \sin \theta }{m}\)