A polarizer only allows light which is vibrating in a particular plane to pass through it. This plane forms the “axis” of polarization. Unpolarized light vibrates in all planes perpendicular to the direction of propagation. If unpolarized light is incident upon an “ideal” polarizer, only half will be transmitted through the polarizer. Since in reality no polarizer is “ideal”, less than half the light will be transmitted.

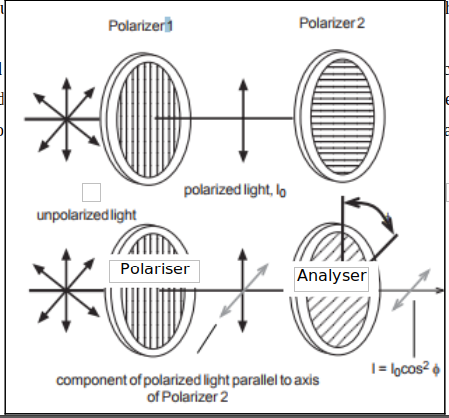
The transmitted light is polarized in one plane. If this polarized light is incident upon a second polarizer(termed as Analyser), the axis of which is oriented such that it is perpendicular to the plane of polarization of the incident light, no light will be transmitted through the Analyser.

However, if the Analyser is oriented at an angle so that it is not perpendicular to the polarizer, there will be some component of the electric field of the polarized light that lies in the same direction as the axis of the Analyser, thus some light will be transmitted through the Analyser (see the above figure). The component, \(E\), of the polarized electric field, \(E_{0}\), is found by:

$$E = E_{0} \cos \phi$$

Since the intensity of the light varies as the square of the electric field, the light intensity transmitted through the second filter is given by:

$$I = I_{0} \cos^{2} \phi$$

Where \(I_{0}\) is the intensity of the light passing through the first filter and \(\phi\) is the angle between the polarization axes.