When a Plano-convex lens of long focal length is placed on a plane glass plate, a thin film of air is enclosed between the lower surface of the lens and upper surface of the glass plate. The thickness of air film is very small at the point of contact and gradually increases from the center outwards. The fringes produced are concentric circles. With monochromatic light, bright and dark circular fringes are produced in the air film. When viewed with white light, the fringes are colored.

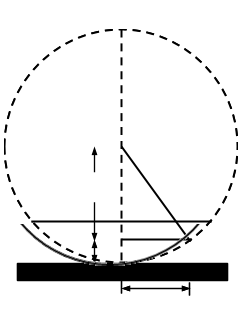
A horizontal beam of light falls on the glass plate at an angle of 45˚. The glass plate reflects a part of the incident light towards the air film enclosed by the lens and plate. The reflected beam from the air film is viewed with a microscope. Interference takes place and dark and bright circular fringes are produced. This is due to the interference between the light reflected at the lower surface of the lens and upper surface of glass plate. For normal incidence the optical path difference between the two waves nearly 2µt, where µ is refractive index of film and t is thickness of the film. Here an extra phase difference of π occurs for the ray, which has got reflected from upper surface of plate because the incident beam in this reflection goes from a rarer to denser medium. Thus the conditions for the constructive and destructive interference are $$2µt= mλ \quad for\; minima; \; m =0, 1, 2, 3…\; (1)$$ $$2µt= (m+12)λ \quad for \; maxima; \; m=0, 1, 2, 3…\; (2)$$ The air film enclosed between the spherical surface of radius R and a plane surface glass plate, gives circular rings such that \( r_{m}^2=(2R-t)t\). Where \(r_m\) is radius of \(m^{th}\) order dark ring. Now \(R\) is of the order of 100 cm and t is at-most 1cm. Therefore, \(R\gg t\). Hence, $$(R-t)^2 +r_{m}^2=R^2 \\ \Rightarrow r_{m}^2=(2R-t)t$$ (neglecting the \(t^2\) term), giving, \( 2t\approx \frac{r_{m}^2}R\) Putting the value of \(2t\) in eq. (1) gives, $$m λ \approx r_{m}^2R \Rightarrow r_{m}^2 \approx mλR,\;m=0, 1, 2….$$ And eq. (2) gives (for the radius \(r_m\) of \(m^{th}\) order bright ring) $$r_{m}^2R=(m+ \frac{1}{2})λ⇒ r_{m}^2=(m+ \frac{1}{2})λR$$ Hence, for dark rings $$r_m= mλR \\ r_m= (m+ \frac{1}{2})λR ;\; m=0, 1, 2….$$ With the help of a traveling microscope, we can measure the diameter of the \(m^{th}\) order dark ring = \(D_m\), Then \(r_m= \frac{D_m}{2}\) and hence, $$D_{m}^2=4mλR$$ So if we know the wavelength \(λ\), we can calculate \(R\) (radius of curvature of lens). For calculating the refractive index of the thin film enclosed between the lower surface of lens and upper surface of glass plate, $$ \mu = \frac{4mλR}{D_{m}^2}$$