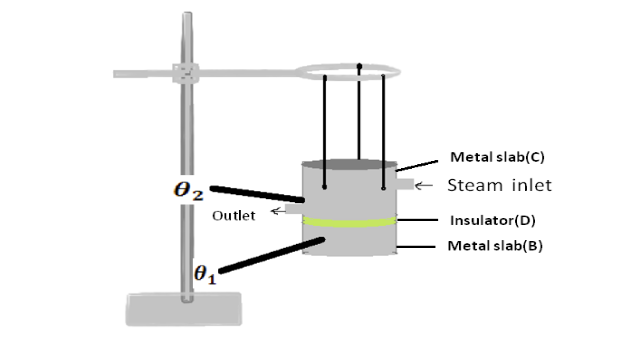
Lee's disc apparatus

The given bad conductor (D) is shaped with the diameter as that of the circular slab B. The bad conductor is placed in between the steam chamber (C) and the disc (B), provided the bad conductor, steam chamber and the slab should be of the same diameter. Holes are provided in the steam chamber (C) and the disc (B) in which thermometers 1,2 are inserted to measure the temperatures.
The total arrangement is hung over the stand as shown in Fig1. When a steady state is reached, let \(\theta_1\) and \(\theta_2\) be the temperatures of metallic disc C and disc B. So, the temperature difference between the two ends of bad conductor is (\( \theta_1 - \theta_2 \)). When the apparatus is in steady state, the rate of heat conduction into metal disk B must be equal to the rate of heat loss due to cooling from the bottom of the disk B. The heat loss can be measured by how fast disk was cooling from steady temperature \(\theta_2\) .
The rate of heat loss = \(\frac{dQ}{dt}=Mc\frac{d\theta}{dt}\)
\(M\)- Mass of disc
\(C\) – specific heat capacity of disc
\(\frac{d\theta}{dt}\) - temperature loss per unit time in \(\theta_2\)
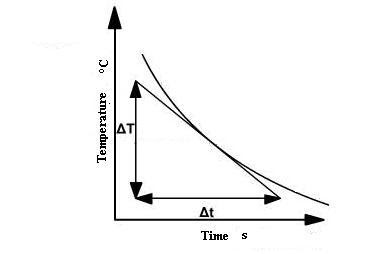
Note : \(\frac{d\theta}{dt}\) can be measured from cooling curve . It is slope of cooling curve of disc B.
Hence, it is equal to thermal conductivity of any substance. The rate of heat conducted through the bad conductor is, $$\frac{dQ}{dt}=\frac{k×A×(\theta_1-(\theta_2)}{L}$$ \(K\) – coefficient of thermal conductivity
\(A\) – area of bad conductor
(\(\theta_1\)- \(\theta_2\)) - temperature difference in steady state
\(L\) – thickness of poor conductor Equating both equations
Thermal conductivity = \(k = \frac{M×c×L×\frac{d\theta}{dt}}{A×(\theta_2-\theta_1)}\)