The volume of a fixed no of moles of atmospheric air is always fixed. The temperature is varied with the use of hot water poured in the cup.
Make the following table in your notebook and fill in the details.
|
S.No |
Physical quantity |
Independent / Dependent |
Measured with |
Measuring instrument’s |
||
|
Minimum |
Maximum |
Least count |
||||
|
1 |
Pressure |
|
|
|
|
|
|
2 |
Volume |
|
|
|
|
|
How to measure pressure:
-
The top point in the open end of manometer is at atmospheric pressure.
-
If the levels in both the arms are at same height, then the gas in the closed arm is also at atmospheric pressure.
-
If the level of mercury in the closed arm is lower than the open end, then the gas in the closed arm is at higher pressure than the atmospheric pressure (PA).
How to measure Volume:
-
The volume of gas is enclosed in a (almost) cylindrical tube. (Neglect the curvature of the closed tube and the surface of mercury).
-
Hence the volume is . Here h = \(h_{3}\)- \(h_{2}\) (as shown in figure given below)
-
As Cross section is constant and volume is proportional to h, take readings for volume in terms of h.
- Place a thermometer in the bath which surrounds the bulb, this will be equal to the room temperature. This will be the temperature of the gas in the bulb as well.
-
Mark a line to indicate the initial volume of the mercury on the closed ended tube. If necessary
adjust the open end of the tube such that mercury level comes close to the lower end of the
bulb. This height will be referred as \(H_{0}\).
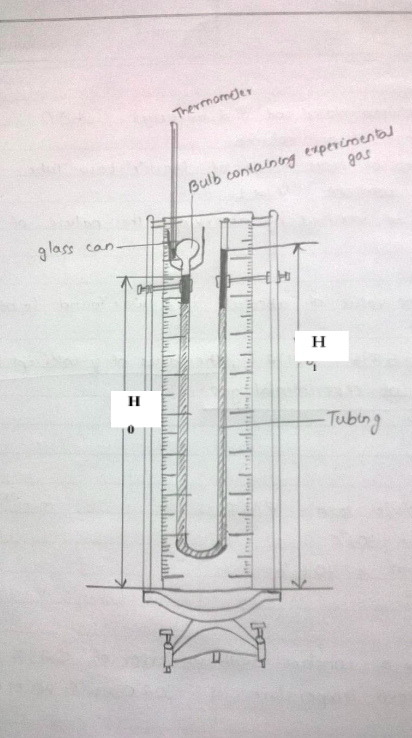
Figure 1: Measurements to be taken - Constant volume gas thermometer apparatus - Boil water in an electric kettle.
- Carefully pour it in the bath such that the gas bulb is completely submerged. And wait for one minute for the gas to reach thermal equilibrium with the bath.
-
While quickly adjusting the height of the open end to bring the mercury level back to \(H_{0}\),
note down -
- The temperature of the bath (This will also be the T of the gas in the bulb).
- Height of the mercury in the open end – \(H_{1}\).
- Time – \(t\)
Table III : Measurements.
\(H_{0}\) = _________ cm
S.No.
Measure
\(\propto\) Pressure
Time
\(T\)
\(H_{1}\)
Δ\(H\)=\(H\)- \(H_{0}\)
s
\(^{\circ}\)C
cm
cm
1
2 …
… 10
- Repeat the measurements of step 5 with intervals of 5 \(^{\circ}\)C, until the temperature cools down to room temperature.
-
Plot the following graphs
- Temperature (T) vs. - Pressure(ΔH)
- Time (t) vs. - Temperature (T)
- Perform the least square fitting of the data in graph A to a straight line.
- Perform the least square fitting of the data in graph B to a exponential decay. The same graph can be plotted as ln(t) vs. Temperature and fit then fit to a straight line.