The graphs on the computer screen would look like this -

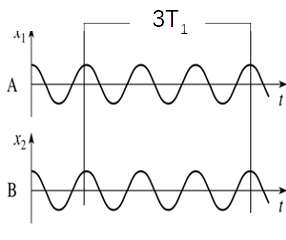
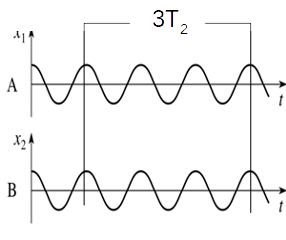
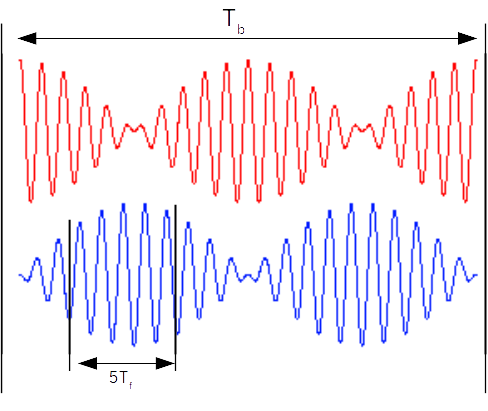
\(\omega_{1}\) and \(\omega_{2} \) can be deduced from the beat graph using this equation- $$\theta(t) = \theta_{0}cos\left[\left(\frac{\omega_{1} - \omega_{2}}{2}\right)t \right]cos\left[\left(\frac{\omega_{1} + \omega_{2}}{2}\right)t\right]$$ $$\omega_{b} = \frac{\omega_{1} - \omega_{2}}{2}$$ $$\omega_{f} = \frac{\omega_{1} + \omega_{2}}{2}$$