Two physical quantities need to be measured in this experiment –time and Length.
Make the following table –
| S.No | Physical quantity | Independent / Dependent | Measured with | Measuring instrument’s | ||
|---|---|---|---|---|---|---|
|
Minimum |
Maximum |
Least count |
||||
|
1 |
Time |
dependent |
stopwatch |
|||
|
2 |
Length |
Independent |
Meter scale |
|||
-
Take two threads of ~ meter length and tie them to hooks of the two bobs separately.
-
Tie the other end of the threads to the hooks mounted on the wall. The separation should be ~ 15 cm.
-
Measure the time period of both the simple pendulums and make a note of them.
-
Connect the two pendulums with a spring/thread at the center (~50 cm from the top).
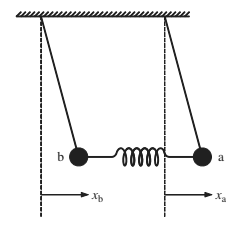
In-phase oscillation
-
Displace both the Pendulums by equal amount in the same direction from the equilibrium position.
-
Let it oscillate freely for 5-6 oscillations.
-
Then, measure the time taken for ten oscillations.
-
Calculate the time taken for one oscillation and hence the frequency.
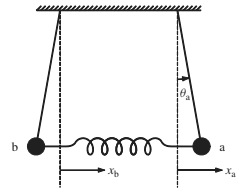
Out of phase oscillations.
-
Repeat the steps 5-8 by displacing the Pendulums by equal amount in the opposite direction from the equilibrium position.
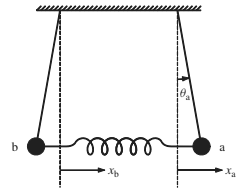
“Beats” oscillations
-
Repeat steps 5-8 by displacing only one of the pendulums.
-
Observe the motion of both the pendulums.
-
Measure the time taken between two subsequent standstills of a pendulum. This is equal to half of the beat period of the coupled oscillator.
-
Calculate the angular beat frequency.
Tables for recording the data
|
Sl. No. |
Time taken for 10 oscillations |
Time period $$T_{1}$$ |
frequency $$f_{1} = \frac{1}{T_{1}}$$ |
Angular frequency $$\omega_{1} = \frac{2\pi}{T_{1}}$$ |
|
1 2 : 10 |
|
Sl. No. |
Time taken for 10 oscillations |
Time period
$$T_{2}$$ |
Frequency $$f_{2} = \frac{1}{T_{2}}$$ |
Angular frequency $$\omega_{2} = \frac{2\pi}{T_{2}}$$ |
|
1 2 : 10 |
|
Sl. No. |
Beats period $$T_{b}$$ |
Beat Frequency $$f_{b} = \frac{1}{T_{b}}$$ |
Angular beat frequency $$\omega_{b} = \frac{2\pi}{T_{b}}$$ |
|
1 2 : 10 |