The word filar means relating to thread or line. The bifilar suspension is a technique used to determine the moment of inertia of any type of object about any point on the object. This is done by suspending two parallel cords of equal length through the object being examined.

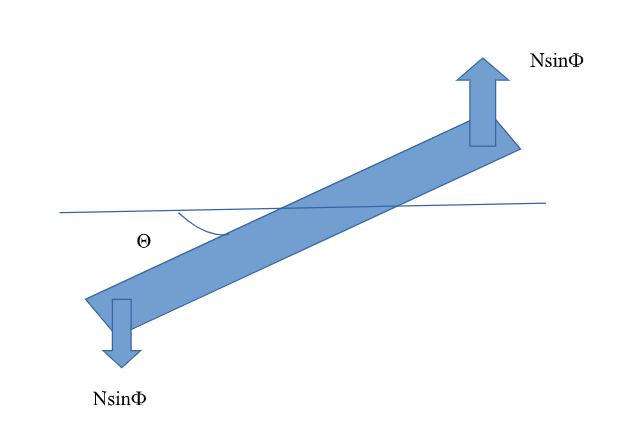
When the block is slightly rotated, the filaments make an angle φ with their original position. Similarly, the block makes an angle θ with its original position. Taking the length of the filament as L and the distance between the points of suspension as 2r, we can equate the displacement of the block as follows

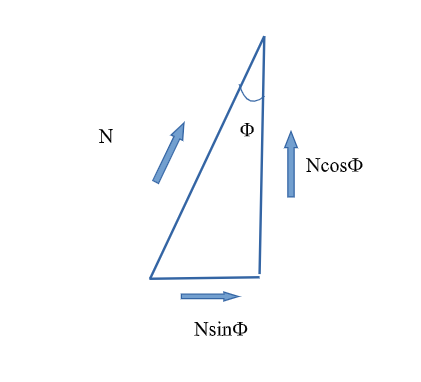
$$ l \phi = r \theta \\ \tau = N * 2r $$

Torque can be calculated as follows

where N (= mg/2) is the tension in the string.

$$ \tau = - 2N r sin \phi \\ I \alpha = -2Nr sin\phi \\ I \alpha = -2Nr \\ I \frac{d^2}{dt^2}\theta = - 2Nr\phi \\ I \frac{d^2}{dt^2}\theta = - 2mgr\phi \\ I \frac{d^2}{dt^2}\theta = - \frac{mgr^2\theta}{L} \\ $$

This is the equation of a simple harmonic oscillator. Therefore, the formula of the time period can be written as follows

$$ T = 2\pi \sqrt{\frac{IL}{mgr^2}} $$

Taking the length of the filament as , half of the distance between the supports as d1, and half of the distance between the lower ends of the filament as d2 we can express the time period as

$$ T = 2\pi \sqrt{\frac{Ih}{mgd_1d_2}} \\ T^2 = 4\pi^2 \frac{Ih}{mgd_1d_2} \\ I = \frac{T^2mgd_1d_2}{4\pi^2h} $$