The Kater’s pendulum is a reversible free-swinging pendulum, with holes placed such that the moment of inertia of one is the same as its counterpart, equidistant from the central hole.

The Pendulum oscillates because of a torque acting on it due gravity. For this rigid body, from the diagram:

$$ -mgsin\theta = I \alpha \\ \Rightarrow I \frac{d^2\theta}{dt^2} + mgsin\theta = 0 $$

using small angle approximation

$$ \Rightarrow I \frac{d^2}{dt^2} + mg\theta = 0 $$ Thus we get, $$T = 2\pi \sqrt{\frac{I}{mgl}}$$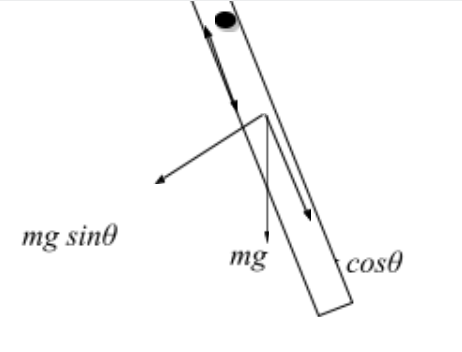

When axis of rotation is not along centre of mass

$$I = I_0 + ml^2 $$

Hence,

$$ T = 2\pi \sqrt{\frac{I_0 + ml^2}{mgl}} \\ I_0 = mk_0^2 \\ T = 2\pi \sqrt{\frac{k_0 + l^2}{gl}} $$

Method 1: Taking T₁ and T₂, corresponding to pairs of holes equidistant from central hole, to be equal, we get,

$$ T_1 = T_2 = T \\ \Rightarrow 2\pi\sqrt{\frac{k_0 + l^2}{gl_1}} = 2\pi\sqrt{\frac{k_0 + l^2}{gl_2}} \\ \Rightarrow k_0 = \sqrt{\frac{l_1^2l_2 - l_2^2l_1}{l_1 - l_2}} = \sqrt{l_1l_2\frac{1 - l_2}{l_1 - l_2}} \\ \Rightarrow k_0 = \sqrt{l_1l_2} \\ T = 2\pi \sqrt{\frac{l1+l2}{g}}\\ g = \frac{4\pi^2}{T}(l_1+l_2) $$

Method 2:

$$ l_2 T_2^2 - l_2T_1^2 = 4\pi^2 \left( \frac{k_0^2 +l_2^2}{g} \right) - 4\pi^2 \left( \frac{k_0^2 +l_1^2}{g} \right) \\ \Rightarrow \frac{4\pi^2}{g} = \frac{l_2 T_2^2 - l_2T_1^2}{l_2^2 - l_1^2} = \frac{T_2^2 + T_1^2}{2(l_2 + l_1)} + \frac{T_2^2 - T_1^2}{2(l_2 - l_1)} \\ \Rightarrow g = 8\pi^2 \left[ \frac{T_2^2 + T_1^2}{(l_2 + l_1)} + \frac{T_2^2 - T_1^2}{(l_2 - l_1)} \right]^{-1} $$