“For relatively small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load.” (Encyclopædia Britannica, n.d.)
In a spring of ‘stiffness’ k (Spring Constant), on applying a force F, there is a displacement y according to Hooke’s Law – $$F=-ky\tag{1}$$
Hence a spring, with no damping, i.e, no loss of energy, executes SHM.
Time period (T) is given by: $$T=\frac{2π}{ω}=2π\sqrt{\frac{m}{k}}$$ $$\begin{align*} &\text{where,}\\ &ω\text{ = angular frequency and}\\ &m\text{ is mass of load} \end{align*}$$ The mass of spring (ms) also influences the SHM, since each unit mass on it experiences a force due the preceding units. The equivalent mass then becomes m≈mload+ms3 (Fox & Mahanty, 1970).
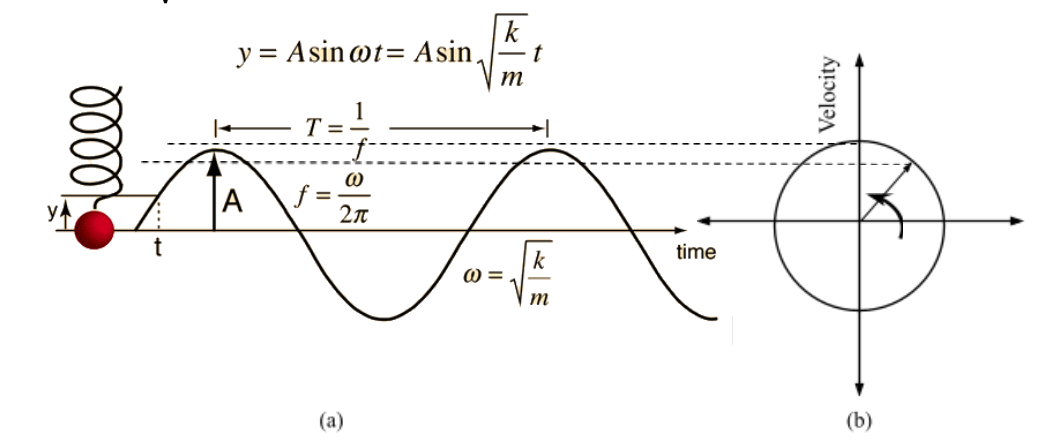
Figure SEQ Figure \* ARABIC 1: Plots for a spring executing SHM (without phase difference)
(a) Position (y) vs Time (t) [Real Space]
(b) Velocity () vs Position (y) [Phase Space]